Risolvere un sistema di equazioni di primo grado non è difficile, se sappiamo esattamente dove mettere le mani. In questo articolo sto considerando sistemi di due equazioni di primo grado a due incognite, detti anche sistemi lineari di due equazioni in due incognite.
Trovare la soluzione di un tale sistema significa trovare i valori numerici che soddisfano contemporaneamente le due equazioni. In parole povere dobbiamo trovare i numeri che vanno bene per entrambe le equazioni.
Per dirlo in maniera rigorosa possiamo ricorrere a questa definizione:
Si chiama sistema di equazioni, nelle stesse incognite, un insieme di equazioni considerate simultaneamente, con lo scopo di sapere se hanno, oppure no, soluzioni comuni e, in caso affermativo, di determinarle.
In pratica come facciamo a risolvere il nostro sistema?
Procediamo prima di tutto con il caso generale.
Supponiamo che i coefficienti delle incognite del sistema:
siano tutti diversi da zero.
In questo caso si può dimostrare che:
Il sistema lineare è:
- determinato, se ab’ – a’b <> 0
- impossibile, se ab’ – a’b = 0 e cb’ – c’b <> 0;
- indeterminato, se ab’ – a’b = 0 e cb’ – c’b = 0.
Quindi questi sono i tre casi che si possono verificare. Naturalmente essi valgono anche quando dovesse capitare che i coefficienti non sono tutti diversi da zero.
Se il sistema è determinato, le soluzioni x e y sono date dalle formule:
Nella pratica è difficile ricordare le due formule precedenti, quindi è meglio ricorrere ad altri procedimenti.
Esistono quattro metodi per risolvere i sistemi di primo grado e sono:
1) Metodo di sostituzione;
In questo caso, una volta che le due equazioni sono state ridotte a “forma normale” cioè sono di questo tipo:
possiamo risolvere una delle due equazioni rispetto a una delle variabili, in questo modo:
e sostituirla nella seconda equazione, in questo modo:
Ora la seconda equazione dipende solo dalla variabile y e la possiamo risolvere:
Ora che abbiamo trovato la y, possiamo di nuovo sostituirla nella prima equazione:
E semplificando troviamo anche la variabile x:
Che non sono altro che le soluzioni fornite all’inizio.
Esempio:
Ricaviamo la x dalla prima equazione:
sostituiamo nella seconda
Poi moltiplichiamo e portiamo le variabili al primo membro e i coefficienti al secondo:
adesso sommiamo e risolviamo rispetto alla y:
Adesso anche abbiamo trovato la y, la sostituiamo nella prima equazione:
Ed ecco la soluzione:
2) Metodo del confronto;
Le due equazioni vengono risolte entrambe rispetto alla variabile x e poi, visto che i primi membri sono uguali (sono entrambi x), ne segue che anche i secondi membri lo sono.
da cui segue:
In cui la prima equazione contiene la sola variabile y.
Esempio:
Ricavando la x da entrambe le equazioni, si ottiene:
ed eguagliando i due valori:
Risolvendo la prima equazione, solo nella variabile y:
alla fine si ottiene:
e sostituendo –1 alla y:
La soluzione pertanto è: x = 3; y = –1.
3) Metodo di addizione (o della combinazione lineare);
Il metodo consiste nel trasformare il sistema:
nel sistema equivalente:
Esempio:
Risolviamo il sistema:
per eliminare la x si moltiplicano i termini della prima equazione per 2 e quelli della seconda per –3:
da cui, sommando membro a membro:
per eliminare la y si moltiplicano i termini della prima equazione per 3 e quelli della seconda per 5:
sommando membro a membro, si ottiene:
queste due equazioni ottenute, riunite, dànno il sistema:
4) Metodo di Cramer.
Anche in questo caso le equazioni devono essere in forma normale.
Con i coefficienti a, b, a’ e b’ possiamo costruire il determinante del sistema:
Se D è diverso da zero, il sistema ammette soluzioni, quindi possiamo calcolare i determinanti della x e della y, nel seguente modo:
Le soluzioni del sistema saranno date dalle formule:
Esempio:
(è lo stesso sistema degli esempi precedenti)
Vediamo che:
Il determinante del sistema è diverso da zero, quindi possiamo procedere a calcolare le soluzioni, che in base a quanto illustrato prima sono:
Che è appunto la soluzione ottenuta con tutti gli altri metodi.
_______________________________________________________
Se questo articolo ti è piaciuto, iscriviti al mio feed. I feed ti permettono di ricevere direttamente sul tuo pc tutti gli articoli del mio blog senza bisogno di visitarlo continuamente! Per maggiori informazioni sui feed, guarda questo filmato.
Leggi anche:
>> Le prime 1000 cifre di pi greco
>> E = mc²: la formula fisica più famosa della storia
>> Algoritmo
>> Forza gravitazionale e forza elettrostatica: analogie e differenze
>> Cucinare un wurstel con l’energia solare
>> I terremoti più forti del mondo a partire dal 1900
>> Velocità della luce. Galileo fu il primo a cercare di misurarla
>> Teorema di Pitagora. Ecco come impararlo facilmente
>> Le teorie scientifiche che hanno cambiato la nostra visione del mondo
>> Le 10 cose più strane che si possono trovare nello spazio cosmico
>> Alcuni ricercatori hanno trovato il gene che causa l'eiaculazione precoce!
>> Un'oca preistorica gigante raggiungeva le dimensioni di un piccolo aereo!
![clip_image002[1] clip_image002[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgodU7VjJc9FwBeraC2AAsYWsxoWdrT3FHRC-xsFdkhJ9A7dACcOxZSG392jHyBiPBJG9Q3owLhsnSFQqYxLJsjB_Eagkmd_4RmYREQpNaVJjyPMq8a5VuGcbqV1bAXAz5t3gCEVZDjo7yZ/?imgmax=800)
![clip_image002[3] clip_image002[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj8Px3zRDYaayXABlCGjJO_-JxW3a-a_gBTTiGxA4ieQQBkOh8ntGXvxo-7FdLlQGey0SMuq8P7TxmUjZ0nAwgVMS_Psa4YOH8ldkGep1lBE92s4G44sOCwnSbZ1oAN-vGhyphenhyphen20r-333A8Q0/?imgmax=800)
![clip_image002[5] clip_image002[5]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiGyIUn4sLmXILxPlDuaK4Kr-C7LYNElYnO-PiTDpUP5NiRMMle8lnTjrzSHfWhnahqv5bKjH8Si_brnNtmDSlxTxwN1tXheHhia2oPZZyz0W4X6noMjD-PdQyvScdG4Pjuu3BIDa6X4NQL/?imgmax=800)
![clip_image002[7] clip_image002[7]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgeEioGUeujtaHXdA8DOBm-TWn37pLQCTWVAfolz_vbTbnIWOrzlGIfmXwC6XtYR8BbhBLJJ1M6nT8VTz2b6ZRsOZR8lpHhBOjw6FygtPz8lKwGxwM436tjAWR7zV8mizCm6YyD-n5RS9x-/?imgmax=800)
![clip_image002[9] clip_image002[9]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgBtCRr1Q_rjOmHsuDtY5mJYU-Wnmk9NOGoFZ2AsZsKrLsysIUDq915fZxJlGqDcLVh-USnASN3yZXyu2P9NVIVjb0eJfGY1PongC8XLdwbOdOzwamUsflrUh_lld26Fv0Dc9BtPC39yZSt/?imgmax=800)
![clip_image002[11] clip_image002[11]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjC1ZbWxX0yhrqxmeQ81pGQCLu9iLxyZEMJNuXam3oTSdkzuVINR5N_DhxadKUSLZ3tyqK7pJrO_DuFXH55EraxZyzEU4bRUof7q_WsbjaVVxYhjtHvcfrRY3bY3ZES7fu6B6qEHC9neaOH/?imgmax=800)
![clip_image002[13] clip_image002[13]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEi-gJnw-4jlxAVh3K4YmkEz8hTwdAcNVJX0fB3EiXYbQhQ8XmLvHI8TCfrI1Q7s4RzQTtY7_BJqLV5wi15K_5Wl31W0RTz9pOtp0wUFFUtf1VjYT6JqBrlpIOl8g6AEwUVh96lN0uxAmJZm/?imgmax=800)
![clip_image002[15] clip_image002[15]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj9i7XZHOu8M-005THdPVXJLyH2PufzK8HYqX-JNvzp7rG7FRJeu1Fd9wiSqBfNf8NxprbhpYoQjkVbgZiman_E_rQOwWKQiCB1mjPgCV_RgBb_h5NDbKyZs8FgUBYuaqvzmIv5RNli6rpq/?imgmax=800)
![clip_image002[17] clip_image002[17]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgCStxIK9CoE60t1kUOb8ktzFbI9IlU-VxIRW-BjKL5vG4yU6IKYHeBHRto6b6jW0YEmKYlz0K_v9ZonzaXzoQmrH2Rphp5Oh3m4AQXssCBTSlaqFxo8doWDsSu6qxley37ons50ALzknjE/?imgmax=800)
![clip_image002[19] clip_image002[19]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEivYdiF7zqKNd81KkxXK5kTUGFn139_8z0ZhIWEEC3D-jxAnR7eL7qu9JZTLYLsUXSkgTbK0ARk-3ZWkowjek67zGcnC_ztgN8X44K4ESLSehbjqIi7idFBOtSHiKcsEx8sIEH4ZnWb2IVT/?imgmax=800)
![clip_image002[23] clip_image002[23]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgo4kV8BtZ3YkuodDAQNJI_6WwtDHCXQ21AVBamzI54Gsk3OAqjyCUfDHhrvZGBkS38zBtltnz1GOpTsqxdFAUZ7W_hY-VfVLikVF6ZSAUcrjAUMepR3OedkMS86mW0faxLK4bXzco2a2_W/?imgmax=800)
![clip_image002[25] clip_image002[25]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjzl_kyc1FRvxjwuJ1Kyhix48NYOf914iAw2XfAG4IcrH_cNx_aYRVLeYdPBiahOnLKkj1BPfSYtj0cRTImSjppqhm_M49NPXhuVgfzGdax1eKR5w_awD1lmBVXGyX-mZ_k2gq5CFuvT-Ca/?imgmax=800)
![clip_image002[27] clip_image002[27]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiRAsMfSQU2y3PlFovm5SgrLxm2d3JFVYHXTIYY6KV9S4m-ODEgeLc_PTmMkugH0aryRzAlBbPdWDLAZqiWbECv2_yOAAetM6C4s3ROwnYQ3ssdCRiNJSHOvsZco4h1O3odFOj0Sw7Mr_hj/?imgmax=800)
![clip_image002[29] clip_image002[29]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgjd4HgEcsrYbpoR3gvZRivV6jE4kk3Wtvr4kabAavhgIkeP3M1Geqx9qq4GyOatRtI9y6PZttlH43JS360k_8eOqmtD_dnAlfW9NtUlH36WQXreD-hhcbg9ipEEmihsxRMnR3PxVj3WBqz/?imgmax=800)
![clip_image002[31] clip_image002[31]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEihuWn-AwcQhS9VOdyu7c1BwQqOHaexqk_cDLg2QBYrrya7GFjodcgmNEgSWY_iEqZYfvjK-wmyC5oiqtJK4Qvzjg7g7dTmkwePLdnRjUTKbBrT94ADpuEmvTGdJgK64ZniJu3cSq5iCwgq/?imgmax=800)
![clip_image002[33] clip_image002[33]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjVy64SyraDceHmm1IqBh2QnTJwE_DkBN3DtEw78HIflx8CoZIBKdESXozxagCm2JaMCxkaa4BB8Fk3bE60aKmwV6zqa3l9sTP1_3CddwLR385a3MDHNhiBhFbkRSYYlSdVYjhsEQ0-PKzK/?imgmax=800)
![clip_image002[35] clip_image002[35]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjsI_AAkHF8nU7UZUtc4KHFWoIeyLjvY9uHh5Ei11-Mq51n7_1RgQXvnrji3Jou9x0RH14wmHi4wOm0PGIwZ4oBduq1rlGoQtswDa4l8NCI8uEhKW0Sr5AxSAVMzHt7vFbY4rTUwAAdazoz/?imgmax=800)
![clip_image002[37] clip_image002[37]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjFyPKIwMr6LqqlYCpVhX0tgPCfzYsBK6kk5MPa0wgAF8pcQfD6Sg_SMU-PhyJrU5dGRaT_-L67gAUhtd7HYd1Gr4w5AlxXTkJxzxQlIHJPEhXLv3vzAHNtOOM_j-8rzGJG_HgEkI2cowfT/?imgmax=800)

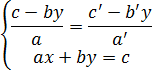

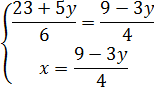


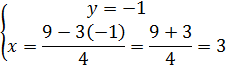



Nessun commento:
Posta un commento
Lascia un tuo commento!