Modelli di geometrie non euclidee

 

Il modello di Klein di geometria iperbolica

Data una circonferenza T (figura sotto), si chiama:

- punto di Klein un qualunque punto P, interno a T;

- retta di Klein una qualunque corda AB di T;

- piano di Klein l’insieme dei punti non esterni a T;

Inoltre:

- due rette di Klein si dicono incidenti se hanno in comune un punto di Klein.

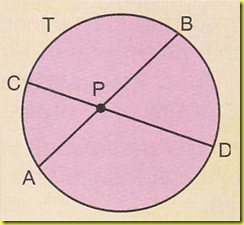
Per esempio nella figura sotto le rette di Klein AB e CD sono incidenti nel punto P di Klein.

 

- due rette di Klein si dicono parallele se hanno in comune un punto di T.

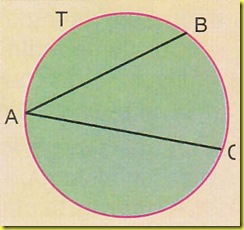
Per esempio le rette AB e AC sono parallele, in quanto si incontrano nel punto A della circonferenza T, come si vede nella seguente figura.

 

Si può dimostrare che questi enti (punti, rette, piano di Klein) verificano gli assiomi della geometria euclidea, escluso l’assioma delle parallele; vale invece la seguente proprietà:

In un piano esistono almeno due rette, passanti per un punto e parallele ad una data retta.

Per esempio (figura sotto) le rette distinte AC e BD passano per P e sono entrambe parallele alla retta AB.

Il modello di Klein prova che l’assioma delle parallele è indipendente dai precedenti assiomi della geometria euclidea.

 

Un modello di geometria ellittica

Data una superficie sferica S, si chiama:

- punto di Riemann ogni coppia di punti estremi di un diametro di S.

Per esempio le coppie (A,B) e (C,D) sono punti di Riemann;

- retta di Riemann ogni circonferenza massima di S.

Per esempio T1 e T2 sono rette di Riemann.

- piano di Riemann la superficie sferica S.

Anche in questo caso, si può dimostrare che questi enti verificano gli assiomi della geometria, escluso l’assioma delle parallele; vale invece il seguente assioma:

In un piano, qualunque retta passante per un punto dato incontra una retta data.

Infatti, due qualsiasi circonferenze massime di S si incontrano sempre in due punti diametralmente opposti.

_________________

Technorati Tag: Riemann,Klein,geometrie non euclidee,geometria ellittica,geometria iperbolica