Una ricerca di psicologia ha accertato che usando il bancomat al supermercato si arriva a spendere fino al 36% in più!

Questa notizia corrisponde esattamente ad una sensazione che ho sempre avuto, senza però prendermi mai la briga di controllare direttamente dalle cifre spese. Per fortuna che ci sono i ricercatori che si prendono il disturbo di fare esperimenti intelligenti! In conlusione, la cosa adesso è sicura: al supermercato si spende molto di più se si pensa di pagare con il bancomat. Lo hanno scoperto i ricercatori dell'università di Chicago: nel loro studio pubblicato dal "Journal of Consumer Research" hanno dimostrato che se si pensa di togliere i soldi dal conto invece che dal portafogli la spesa aumenta in media del 36%. La nostra sensazione "istintiva" quindi è perfettamente giusta :-)
I ricercatori hanno chiesto all'ingresso di un supermarket ad alcuni clienti di dire quanti soldi avevano nel portafogli, mentre ad altri quanto avevano in banca. All'uscita, i primi, che avevano pensato su piccola scala, avevano speso meno dei secondi.
La cosa interessante è anche che lo stesso meccanismo vale per le calorie. In un altro esperimento sono stati offerti dei cioccolatini, indicando ad alcune persone a che percentuale delle calorie del giorno corrispondevano, mentre ad altre a che percentuale delle calorie della settimana. In questo caso quelli che pensavano più in grande hanno mangiato addirittura il 118% in più di cioccolatini. "L'effettiva spesa non dipende dal benessere assoluto, ma dalla percezione - scrivono gli autori - ad esempio, in vacanza si è più portati a spendere perché si tengono più soldi in portafogli".

Amanda Knox. Il fascino del (probabile) mostro. Era già successo anche con Erika (e Omar) e con Pietro Maso.

Non è solo bella, ma anche sospettata di un torbido omicidio. Riceve lettere di ammiratori e molti sono già perdutamente innamorati di lei. Non è la prima volta che succede una cosa del genere, era già successo per la giovane Erika de Nardo nel non lontano 2001. La allora sedicenne Erika, con la complicità del suo ragazzo Omar Mauro Favaro (17 anni), uccise a coltellate la madre ed il fratellino.

La differenza è che Erika è sicuramente colpevole, invece Amanda è solo sospettata. Ma ciò è già sufficiente per scatenare una valanga di messaggi da parte di ammiratori.

Ma non basta. Nell’aula bunker della Corte di Assise di Appello di Venezia, quando veniva celebrato il processo al matricida e parricida Pietro Maso (delitto che risale al 1990), erano presenti, fra gli altri, esponenti dei “Maso fans club”.

Come mai gli assassini (veri o presunti che siano) hanno tanti ammiratori?

Spesso gli psicologi hanno fatto sforzi enormi per comprendere questo fenomeno di "identificazione", senza mai raggiungere risultati davvero convincenti. Molti degli ammiratori dichiarano persino di comprendere le motivazioni che hanno mosso gli assassini! Non è facile capire come e perché qualcuno possa amare un assassino; una cosa sola mi viene in mente: si tratta di qualcosa di inquietante.

La "luce zodiacale". Un fenomeno celeste difficile da osservare.

La luce zodiacale può manifestarsi nella forma di un debole cono di luce che sale dall'orizzonte dopo il tramonto o prima del levar del Sole. Essa si estende sino a grande distanza dal Sole e in generale è osservabile per un periodo abbastanza breve solo dopo che il Sole è scomparso o prima che si sia affacciato all'orizzonte. In una notte limpida senza Luna, in condizioni ideali la luce zodiacale può contribuire per un terzo alla luminosità totale del cielo, e può essere più luminosa della regione media della Via Lattea. Essa è dovuta a particelle disseminate nel Sistema Solare lungo il piano principale del sistema e in prossimità di esso. Il diametro delle particelle è dell'ordine di 0,1-0,2 µm. (Un micrometro è uguale a un milionesimo di metro.) Poiché la luce zodiacale si estende lungo l'eclittica, è visibile particolarmente bene quando l'eclittica è più vicina alla verticale rispetto all'orizzonte, ossia fra febbraio e marzo e di nuovo fra settembre ottobre, agli equinozi di primavera e d'autunno.
La luce zodiacale fu scoperta da G. D. Cassini nel 1683. Egli suggeri correttamente che doveva essere causata da luce del Sole riflessa da «polvere» interplanetaria. (Un accenno alla luce zodiacale potrebbe perà trovarsi già in una quartina del poeta e scienziato persiano Omar Khayyam, vissuto fra l'XI e il XII secolo, che la chiama «fantasma del falso mattino».)

Disturbo d'ansia generalizzato. Uno dei disturbi psichici più diffusi.

Quando una preoccupazione infondata e persistente diventa la reazione di una persona alla maggior parte delle situazioni, tale persona potrebbe soffrire di disturbo d'ansia generalizzato (GAD). Le persone che soffrono di GAD sono affette da ansia e preoccupazione immotivate ed eccessive verso le circostanze della vita (ad esempio, preoccupazioni su questioni finanziarie anche in assenza di "conti in rosso" o di grossi debiti). I pazienti affetti da GAD si sentono spesso insicuri, sostenendo di avere "i nervi tesi" e a volte di provare "un gran vuoto" a causa della tensione che sentono.

I sintomi psicologici del GAD sono inquietudine cronica ed esagerata, agitazione, tensione e irritabilità, che sembrano non avere alcuna causa, o che sono più intensi del normale in una data situazione. Le persone affette da GAD possono anche soffrire di problemi di concentrazione e di disturbi durante il sonno o la veglia. Oltre a questi sintomi psicologici, si manifestano spesso sintomi a livello fisico come tremori, mal di testa, capogiri, spasmi, tensione muscolare, dolori, disturbi addominali e sudorazione eccessiva.

L'ansia dovuta a una situazione reale, come i problemi finanziari conseguenti alla perdita del lavoro, non è un segno di GAD. La caratteristica essenziale del GAD è una preoccupazione persistente che non è una reazione logica alla situazione, e non è legata a nessun altro disturbo d'ansia. Un'ansia cronica ed eccessiva, relativa a situazioni che difficilmente si presenteranno diventa invece preoccupante. Inoltre, l'ansia nei soggetti affetti da GAD è difficile da controllare e causa notevoli complicazioni nella vita lavorativa quotidiana e nell'ambito sociale.

La maggior parte di coloro che soffrono di GAD sostengono di essersi sentiti ansiosi per tutta la vita, e il disturbo si manifesta spesso per la prima volta durante l'infanzia o l'adolescenza. Tuttavia l'insorgenza del disturbo in età adulta non è raro.

Gli esperti pensano che il GAD sia probabilmente causato da una combinazione di fattori biologici e di eventi della vita. Molte persone affette da GAD soffrono anche di altri disturbi medici, come depressione e/o attacchi di panico, che sembrano comportare cambiamenti nella chimica cerebrale, in particolare alcune anomalie relative ai livelli del neurotrasmettitore serotonina.

L'ansia è tra i disturbi mentali più curabili. Cure efficaci comprendono la terapia cognitivo-comportamentale, tecniche di rilassamento e "biofeedback" per controllare la tensione muscolare. In alcuni casi ci può essere bisogno anche di ricorrere ai farmaci. I farmaci ansiolitici più comunemente usati sono le benzodiazepine, come diazepam, alprazolam e lorazepam. Altri farmaci, come il buspirone, possono essere utili per alcuni soggetti.

(Fonte)

Gabriele Sandri non era un tifoso, era soprattutto un ragazzo. Secondo me non esiste un tifo sano: il tifo è sempre una malattia!

Sarà perché odio il calcio sin da quando ero bambino, ma io non riesco a capire bene perché solo con il calcio avvengono questi episodi di violenza. Ci sono appassionati sfegatati di automobilismo, atletica, motociclismo, tennis, basket, pallavolo, curling, sci, ecc... ma mai che si sia sentito che vanno in giro a distruggere tutto ogni volta che si arrabbiano!

In questo caso si è perso di vista completamente che Gabriele Sandri era soprattutto un ragazzo. Mi assale l'amaro sospetto che se non fosse stato un tifoso di qualche banale club calcistico, la notizia della sua morte non avrebbe avuto lo stesso impatto mediatico. Tuttavia, se non fosse stato un tifoso, siamo pur certi che gli ultras non avrebbero messo a ferro e fuoco l'intera città di Roma!

E penso anche a povero agente responsabile di questa tragedia. La sua responsabilità è ovviamente gravissima, ma se Gabriele non fosse stato un tifoso, lo ripeto ancora una volta, non sarebbe mai stato accusato addirittura di "omicidio volontario"!

A questo punto mi viene spontanea una riflessione: non esiste un tifo patologico e un tifo "pulito". Il tifo è pur sempre una malattia. Il tifoso, anche quando non è violento, è comunque una persona con una mentalità abbastanza ristretta, che ha come unico obiettivo quello di essere "folla", chi sta nella folla è un undividuo disperatamente solo. All'interno delle tifoserie i soggetti sono uniformati a pensare allo stesso modo, vestire allo stesso modo, parlare allo stesso modo (in maniera spesso colorita), ripetere gli stessi slogan. Anche la percezione del dolore è alterata in maniera preoccupante. Ho conosciuto una ragazza che, dopo che la sua squadra del cuore era scesa in serie B, ha detto: "mi sono rovinata tutta l'estate!". Molti arrivano a piangere per una sconfitta della propria squadra in maniera più disperata che se fosse morto un parente!

E poi ci sono quelli violenti... ma di costoro abbiamo visto le imprese in tutti i telegiornali.

Come si fa a misurare la distanza delle stelle

Spesso si sente dire che una certa stella dista da noi un certo numero di anni luce. Ma come fanno gli astronomi a misurare la distanza delle stelle?

In effetti esistono vari metodi per avere una valutazione della distanza delle stelle. Si tratta comunque di una stima che prevede un certo grado di incertezza, come accade in qualsiasi misura scientifica.

I metodi più usati sono tre:

1) Metodo della parallasse. Si tratta di un metodo trigonometrico e funziona bene per le stelle più vicine (al massimo un centiniaio di anni luce).

2) Metodo delle Cefeidi. Le stelle variabili dette cefeidi presentano un periodo che è in stretta relazione con la loro luminosità assoluta; dal periodo osservato di una cefeide si ricava quindi la magnitudine assoluta e dal confronto con quella apparente la distanza.

3) Metodi spettroscopici. L'analisi dello spettro di una stella fornisce tra le altre cose una buona stima della sua magnitudine assoluta; il confronto con la magnitudine apparente fornisce una stima della distanza.

La distanza delle stelle più vicine (entro 100 anni luce circa) si misura con il metodo della parallasse.
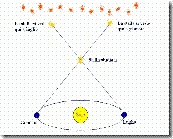
Per metterlo in pratica si deve misurare due volte la posizione di una stella (rispetto alle stelle più deboli e quindi presumibilmente molto più lontane) a distanza di sei mesi. In questo periodo la Terra ha percorso metà della propria orbita, e quindi la seconda osservazione viene fatta a circa 300 milioni di Km di distanza dalla prima (il raggio dell'orbita terrestre è di circa 150 milioni di Km).

A causa di questo spostamento della Terra, che è il punto d'osservazione, si può constatare una modificazione apparente della posizione della stella rispetto alle stelle di sfondo. La misura precisa dell'angolo di spostamento (che per definizione è il doppio della parallasse) permette di risalire alla distanza della stella.

La relazione tra la distanza e la parallasse è data dalla formula:

d = r / sen p

nella quale d è la distanza della stella, r è la base di triangolazione (ovvero il semiasse maggiore dell'orbita terrestre, pari a 149597870 km) e p è l'angolo di parallasse.

Per misurare distanze maggiori di un centinaio di parsec e quindi, in definitiva, per fissare la scala delle distanze nell'Universo osservabile bisogna ricorrere a metodi diversi dalla parallasse. In base alla relazione che sussiste tra la magnitudine apparente e quella assoluta ecco che è necessario scoprire nelle altre galassie delle "candele" stellari, di luminosità assoluta nota, per potere effettuare una stima della loro distanza.

Conoscendo la legge con cui si attenua la luce in base alla distanza ecco che si può risalire, una volta nota la luminosità (o magnitudine) assoluta della stella alla sua distanza.

Uno di questi metodi è quello delle Cefeidi classiche. Chiaramente questo metodo si può applicare a galassie non troppo lontane in quanto condizione fondamentale è che in esse si possano risolvere le stelle che le compongono. Le variabili Cefeidi sono stelle pulsanti con periodi che vanno da 2 a 40 giorni. La signora Leavitt nel 1912 trovò, dopo avere effettuato centinaia di misure delle variabili Cefeidi nelle nubi di Magellano, una relazione tra il periodo P e la magnitudine assoluta Mv. In altri termini le Cefeidi più brillanti variano di luminosità più di quelle meno brillanti e quindi è possibile risalire dal periodo di variabilità alla magnitudine assoluta. Dal momento che la magnitudine apparente è sempre disponibile viene ad essere noto immediatamente il modulo di distanza e quindi la distanza stessa. Per questo motivo le Cefeidi sono dette indicatori di distanza o candele standard.

Scritto il primo manuale di Cold Reading, l'arte in cui si crea l'illusione di sapere tutto della persona che ci si trova davanti (passato, pr

Manuale di cold reading

Come fingere di sapere tutto sul conto degli altri
Introduzione di James Randi

di Ray Hyman

Ho tentato di creare questo volume come un manuale onnicomprensivo sulla lettura a freddo e sulla lettura psichica. Sono convinto che esso contenga tutto quello che vi occorre sapere per comprendere e realizzare letture di successo. Vi suggerirei di prenderlo a piccole dosi. Molto probabilmente riuscirete ad avere successo come lettori “psichici” mettendo in pratica solo uno o due dei suggerimenti contenuti in questo libro.
Col tempo, vi renderete conto che le vostre letture superano di gran lunga quelle del lettore medio che esercita questo mestiere quotidianamente.
Il mio intento non è fornire al mondo nuovi “sensitivi”. Piuttosto desidero impressionarvi con il potere di questa situazione sociale in miniatura. Vi fornirò i dieci “segreti” della cold reading. Perché proprio dieci? Riconosco che non c’è nulla di magico in questo numero. Avrei potuto elencare i cinque o i venti segreti della lettura a freddo. In effetti, sono del parere che in realtà non esiste nessun segreto della lettura a freddo. Può farlo chiunque. E virtualmente qualunque metodo per metterla in pratica “funzionerà”. E davvero possiamo comprimere tutti i consigli in un singolo segreto: provateci! Se sapete parlare, sarete in grado di effettuare una cold reading di successo.

Ray Hyman

Per maggiori informazioni su questo libro, visitate qui e qui.

Le donne serial killer devono lavorare il doppio per raggiungere la notorietà

In questo mondo pieno di ingiustizie le donne ancora non vengono riconosciute nel loro lavoro. E' successo anche a Barbara Louise Huxley, che per raggiungere la copertina di Time e Newsweek, a 46 anni, ha dovuto uccidere il doppio di vittime innocenti rispetto ai suoi colleghi serial killer di sesso maschile. Per lei è stato davvero faticoso raggiungere la notorietà...

Huxley, nella casa di cura dove svolge il suo duro lavoro e i terribili omicidi, ha visto le sue attività non riconosciute per anni.

La sua prima vittima l'ha uccisa a soli 27 anni. Si trattava di un paziente anziano che ha soffocato con i tubi chirurgici. Poi sono seguiti altri sette omicidi per soffocamento, ancora più lenti e metodici.

Come molte giovani donne che vogliono semplicemente la possibilità di uccidere il maggior numero possibile di vittime, prima di essere arrestata dalla polizia, Huxley ha affrontato una feroce resistenza ad ogni turno, a volte da funzionari di polizia, a volte testimoni oculari, o spesso, la resistenza stessa delle vittime.

Huxley ha detto: "Voglio solo essere trattata come qualsiasi altro omicida sociopatico."

Nel frattempo, Huxley e una mezza dozzina di altre donne come lei deve continuare a bruciare e mutilare innumerevoli vittime, senza l'attenzione dei mezzi di comunicazione senza la giusta applicazione della legge che i loro atroci atti giustamente meritano.

Adesso Huxley sogna di essere trattata come un assassino sanguinario e non più, come questa nostra società malata fa, una semplice, dolce tenera donna.

(Fonte)

La mappa di tutti i vulcani attivi nel mondo

I vulcani non sono distribuiti in modo casuale sulla superficie terrestre, ma sono indicatori di zone di debolezza corrispondenti ad aree instabili della crosta terrestre. Essi si trovano in corrispondenza dei limiti di placca, sia dove si crea nuova crosta in risalita dall'astenosfera (dorsali oceaniche) sia dove la crosta viene distrutta sprofondando di nuovo nell'astenosfera (zone di subduzione).
Ne è prova di ciò la cosiddetta Cintura di fuoco che è la linea di vulcani che circonda tutto l'oceano Pacifico. Essa è costituita da vulcani dalla bella forma conica e con pendii abbastanza acclivi. La loro attività è di tipo esplosiva e i magmi eruttati, piuttosto viscosi, sono per lo più di tipo andesitico (da ciò viene chiamata anche linea dell'andesite). Dato il tipo di attività questi vulcani sono caratterizzati da una pericolosità piuttosto elevata.
A questo tipo di vulcani appartengono il Vesuvio (il vulcano a rischio più elevato dell'Europa), i Campi Flegrei, Stromboli e Vulcano nelle isole Eolie.
I vulcani delle dorsali, invece sono caratterizzati da magmi meno viscosi e sono quindi più fluidi. La loro forma è piuttosto appiattita e formano grandi espandimenti lavici. Sono caratterizzati da una pericolosità modesta. Una zona dove è possibile osservare questo tipo di vulcanismo è l'Islanda, in quanto si può considerare un tratto di dorsale affiorante dall'oceano Atlantico. A questo tipo di vulcani appartiene l'Etna, il vulcano più grande d'Europa.
Un vulcanismo simile a quello delle dorsali è dato dai vulcani delle cosiddette rift valleys che rappresentano una dorsale in via di formazione. Questo tipo di vulcani si può osservare in Africa Orientale nella zona dei grandi laghi.
Oltre a questi due grandi tipi di vulcani dei limiti di placche ve ne sono altri tra cui quello dei cosiddetti vulcani di hot spot, che sono situati all'interno di una placca. Appartenenti a questo tipo di vulcanismo abbiamo i vulcani delle isole Hawaii localizzati in mezzo alla grande placca dell'oceano Pacifico. La loro attività è simile al vulcanismo delle dorsali oceaniche.

Per maggiori informazioni visitate la fonte.

Ettore Majorana. Il geniale fisico scomparso misteriosamente nel 1938.

«Al mondo ci sono varie categorie di scienziati; gente di secondo e terzo rango, che fanno del loro meglio ma non vanno lontano. C'è anche gente di primo rango, che arriva a scoperte di grande importanza, fondamentale per lo sviluppo della scienza. Ma poi ci sono i geni come Galileo e Newton. Ebbene Ettore era uno di quelli. Majorana aveva quel che nessun altro al mondo ha. Sfortunatamente gli mancava quel che è invece comune trovare negli altri uomini: il semplice buon senso.»

(Enrico Fermi)

Con queste parole il premio Nobel della Fisica, Enrico Fermi, descriveva il giovane Ettore Majorana. In effetti Ettore era un giovane e geniale fisico, dal carattere ombroso e riservato. Nel 1937 Ettore Majorana fu nominato professore di Fisica teorica all'Università di Napoli, dove si legò d'amicizia con Antonio Carrelli, professore di Fisica sperimentale presso lo stesso Istituto di Fisica.

Ma ciò che fa di Majorana un genio davvero particolare, non era tanto il suo carattere eccentrico, ma la storia della sua scomparsa, tuttora completamente avvolta nel mistero.

La sera del 25 marzo 1938 Ettore Majorana partì da Napoli con un piroscafo della società Tirrenia alla volta di Palermo, ove si fermò un paio di giorni: il viaggio gli era stato consigliato dai suoi più stretti amici, i quali lo avevano invitato a prendersi un periodo di riposo.

Il giorno stesso, prima di partire, aveva scritto a Carrelli la seguente missiva:

Caro Carrelli, Ho preso una decisione che era ormai inevitabile. Non vi è in essa un solo granello di egoismo, ma mi rendo conto delle noie che la mia improvvisa scomparsa potrà procurare a te e agli studenti. Anche per questo ti prego di perdonarmi, ma soprattutto per aver deluso tutta la fiducia, la sincera amicizia e la simpatia che mi hai dimostrato in questi mesi... Ti prego anche di ricordarmi a coloro che ho imparato a conoscere e ad apprezzare nel tuo Istituto...; dei quali tutti conserverò un caro ricordo almeno fino alle undici di questa sera, e possibilmente anche dopo.

Ai familiari aveva invece scritto:

Ho un solo desiderio: che non vi vestiate di nero. Se volete inchinarvi all'uso, portate pure, ma per non più di tre giorni, qualche segno di lutto. Dopo ricordatemi, se potete, nei vostri cuori e perdonatemi.

Il 26 marzo Carrelli ricevette da Majorana un telegramma in cui gli diceva di non preoccuparsi di quanto scritto nella lettera che gli aveva precedentemente inviato.

Lo stesso giorno fu scritta e spedita anche questa ultima lettera:

Palermo, 26 marzo 1938 - XVI Caro Carrelli, Spero che ti siano arrivati insieme il telegramma e lettera. Il mare mi ha rifiutato e ritornerò domani all'albergo Bologna, viaggiando forse con questo stesso foglio. Ho però intenzione di rinunziare all'insegnamento. Non mi prendere per una ragazza ibseniana perché il caso è differente. Sono a tua disposizione per ulteriori dettagli.

Ma Ettore non comparve più.

Iniziarono le ricerche. Del caso si interessò, dietro pressioni di Fermi, lo stesso Mussolini; fu anche proposta una ricompensa (30.000 lire) per chi ne desse notizie, ma non si seppe mai più nulla di lui, almeno non in modo inequivocabile.

Il professor Vittorio Strazzeri dell'Università di Palermo asserì di averlo visto a bordo alle prime luci dell'alba del 27 marzo mentre il piroscafo sul quale era imbarcato si accingeva ad attraccare a Napoli (in realtà egli condivise la cuccetta con un giovane viaggiatore che, secondo la descrizione, corrispondeva a Majorana, da lui mai conosciuto personalmente prima di allora). Un marinaio asserì di averlo scorto, dopo aver doppiato Capri, non molto prima che il piroscafo attraccasse, e la società Tirrenia, anche se l'episodio non fu mai confermato, asserì che il biglietto di Majorana era tra quelli testimonianti lo sbarco. Anche un'infermiera che lo conosceva sostenne di averlo visto, in questo caso nei primi giorni dell'aprile 1938, mentre camminava per strada a Napoli.

Ma non fu mai trovata nessuna traccia documentata della sua destinazione ed in mare non fu mai trovato.

Le indagini furono condotte per circa tre mesi e si estesero ad un convento di Gesuiti che si trovava vicino a dove lui abitava, dove pare si fosse rivolto per chiedere una qualche sorta di aiuto, forse come reminiscenza del suo periodo scolastico presso i Gesuiti di Roma. La famiglia seguì anche una pista che sembrava portare al Convento di S.Pasquale di Portici, ma alle domande rivoltegli il padre guardiano rispose con un enigmatico: "Perché volete sapere dov'è? l'importante è che egli sia felice".

Ci fu una ridda di ipotesi, di indizi, ma non si ebbero mai certezze sulla sorte di Majorana: va comunque notato che nelle sue lettere egli non parla mai di suicidio, ma solo di scomparsa, ed era persona attenta alle parole.

L'unica certezza tra tante supposizioni consiste nel non indifferente prelievo di una considerevole somma di denaro (alcuni stipendi arretrati) che Majorana fece prima di far perdere le sue tracce, l'equivalente di circa 10 mila dollari attuali, oltre che della sparizione del suo passaporto. Anche questo fatto, unito alla razionalità della mente di Majorana, rende poco probabile l'ipotesi del suicidio.

Amaldi nel suo Ricordo scrisse che egli aveva saputo trovare in modo mirabile una risposta ad alcuni quesiti della natura, ma che aveva cercato invano una giustificazione alla vita, alla sua vita, che era per lui di gran lunga più ricca di promesse di quanto non lo sia per la stragrande maggioranza degli uomini.

Il giorno prima di salpare da Napoli consegnò alla studentessa Gilda Senatore una cartella di materiale scientifico: questi documenti furono mostrati anni dopo al marito di questa, anch'esso fisico. Questi ne parlò con Carrelli che ne parlò con il rettore che li volle: dopo di che le carte si persero.

La storia dell’ultimo teorema di Fermat e della sua dimostrazione è una vicenda più appassionante di una saga, più intricata di una tragedia, più affa

La storia dell’ultimo teorema di Fermat e della sua dimostrazione è una vicenda complicata ed è più appassionante di una saga, più intricata di una tragedia, più affascinante di un romanzo d’avventura.

L’Ultimo Teorema di Fermat ha un collegamento forte con la matematica dell’antica Grecia e con i fondamenti del pensiero di Pitagora. Si arriva, in un magico balzo di secoli, dal teorema di Pitagora fino alla sofisticata matematica moderna. Ma vediamo di descrivere, a grandi linee, questa storia così piena di sorprese.

Il problema dell’Ultimo Teorema (da questo momento in poi lo chiameremo così) sembra molto semplice perché si basa su una nozione matematica che tutti possono ricordare:

In un triangolo rettangolo il quadrato costruito sull’ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti.

Questa è la formulazione del Teorema di Pitagora, che tutti conosciamo. Se x, y e z (z è l’ipotenusa e x e y i cateti) sono le lunghezze dei lati del triangolo, allora il teorema può essere enunciato simbolicamente nel seguente modo:

z^2 = x^2 + y^2

Se in un triangolo rettangolo x = 3 e y = 4 si vede che z (l’ipotenusa) sarà uguale a 5, infatti, considerando la formula appena scritta si avrebbe:

52 = 32 + 42 e cioè: 25 = 9 + 16

e per questo triangolo il Teorema sarebbe verificato. Ma Pitagora come poteva sapere che il suo teorema era valido per qualsiasi triangolo rettangolo? Ovviamente non poteva misurare l’infinita varietà di trangoli per vedere se tutti lo verificavano! Tuttavia egli era assolutamente sicuro della universalità delle sue conclusioni. La ragione di questa fiducia sta nel concetto di dimostrazione matematica. La ricerca di una dimostrazione di questo genere è la ricerca di una conoscenza più assoluta di qualsiasi altra conoscenza accumulata da ogni altra disciplina. Il Teorema di Pitagora è una verità definitiva che nessuno potrà mai modificare.

Dopo la morte di Pitagora, i suoi allievi, oltre alla dimostrazione del Teorema, divulgarono al mondo il segreto per trovare le cosiddette “Terne Pitagoriche”. Le terne pitagoriche sono combinazioni di tre numeri interi che soddisfano l’equazione di Pitagora z^2 = x^2 + y^2 . Come abbiamo visto prima l’equazione è valida se x = 3, y = 4 e z = 5. Ma anche se x = 5, y = 12 e z = 13, infatti si ha: 132 = 52 + 122, cioè 169 = 25 + 144.

Un terna pitagorica più grande è x = 99, y = 4900 e z = 4901. Per numeri più grandi le terne diventano sempre più difficili da trovare. Per scoprire le terne i pitagorici inventarono un metodo e nel far questo dimostrarono che il loro numero era infinito. Quindi esistono infinite terne di numeri interi che soddisfano l’equazione di Pitagora. Ma adesso consideriamo una equazione del tipo:

z^3 = x^3 + y^3

dove i quadrati sono diventati cubi. La potenza è passata da 2 a 3. A questo punto ci chiediamo: esistono terne pitagoriche che soddisfano questa equazione? Ebbene, trovare soluzioni per l’equazione “al cubo” sembra proprio che sia impossibile! E inoltre, se la potenza viene cambiata da 3 ad un qualunque numero più alto n (cioè 4,5,6...), anche in questo caso sembra impossibile trovare una soluzione. Alla fine l’equazione:

z^n = x^n + y^n per n maggiore di 2

non riesce più a mostrare soluzioni. E infatti il grande matematico francese del Seicento Pierre de Fermat fece la stupefacente affermazione che la ragione per la quale nessuno poteva trovare una soluzione era che la soluzione non esisteva affatto.

“Dispongo di una meravigliosa dimostrazione di questo teorema, che non può essere contenuta nel margine troppo stretto della pagina”.

Così scriveva Pierre de Fermat a proposito di quello che sarebbe stato il più grande rompicapo degli ultimi quattro secoli. La dimostrazione che non stava nel margine troppo stretto non fu mai trovata. Qui comincia la grande avventura, e quella frase divenne il guanto di sfida raccolto da generazioni di matematici, che si sforzarono invano di dimostrare questo teorema così apparentemente semplice, ma in realtà così impenetrabile.

Dopo oltre tre secoli e mezzo, l’enigma ha trovato una soluzione: un matematico inglese, di nome Andrew Wiles, della Princeton University, che sin dalla sua infanzia sognava di trovare una soluzione, è riuscito nel 1994 a violare il grande segreto.

Resta però ancora un piccolo mistero… Osservando la dimostrazione dell’Ultimo Teorema di Wiles, si nota che è una dimostrazione davvero molto lunga e complicata, che fa uso delle tecniche matematiche più moderne e complesse, molte delle quali sono state introdotte dallo stesso Wiles. Quasi tutte queste tecniche erano completamente sconosciute all’epoca di Pierre de Fermat. Allora ci chiediamo: come aveva fatto il grande matematico francese a dimostrare quel teorema? Aveva forse commesso un errore? Si era ingannato? Oppure esiste un modo molto più semplice per dimostrarlo, che per tre secoli e mezzo è sfuggito anche alle più grandi menti matematiche?

Vorrei concludere con una curiosità, per così dire, “umoristica”. Nella metropolitana di New York, sui muri della stazione dell’Ottava Strada, compare un simpatico graffito, ispirato senza dubbio da tutta l’attenzione dei media per il teorema quando ne fu dato annunzio nel 1994:

“ z^n = x^n + y^n: nessuna soluzione.

Ho scoperto una dimostrazione meravigliosa di questo fatto, ma adesso non posso scriverla perché sta arrivando il mio treno”.